February
17, 2001
Nagging
Math Mysteries
by Pearl Tesler
The
best part about going to conferences like AAAS is that you really
never know what you're going to get. Sure, there are the session titles,
but invariably these, like horoscopes, have been broadly crafted to
apply to a full range of possibilities.
Take
"New Tests for Science". You could show up at this one expecting
just about anything. Maybe there's literally a new test, something
like a geeks' breathalyzer. Or maybe Science as a whole is facing
a grave new challenge, like dissolution of the National Science Foundation,
funder of all great and small. Or maybe they've isolated a science
gene, using samples of Einstein's preserved brain.
It was
in this "don't know what it is but it sounds good" spirit that I showed
up at "The Nature and Origins of Mathematical Thought."
Memorable gleanings related to this stated topic are nil. However,
thanks to a few tangential asides, not one but two math mysteries
that have dogged my days—and perhaps yours?—were finally
solved.
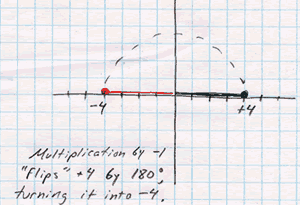
Mystery
#1: Why is it that a negative number times a negative number is a
positive number?
Now, there is some logic to the fact that a negative
times a positive is negative. You can think of (-5) x 2 as two negative
fives, which add up to negative ten. But a negative times a negative?
Math
Mystery #1
The
"aha" comes when you think of these numbers on a number
line. Multiplication by a negative number is like a 180° rotation
about the origin. So if you were pointing in the positive direction,
multiplication by a negative "flips" you, so now you point in the
negative direction. So if you're already negative, multiplication
by another negative number flips you 180°, back to positive. Two
negative multipliers are like a full 360° rotation, putting you
right back where you started.
Mystery
#2: Where did imaginary numbers come from, and why do we graph them
on the vertical axis?
This is one of those dogmas that gets handed
to you in trig. The square root of 1 is 1, and the square root of
-1 is i, an imaginary number. You put real numbers on the horizontal
number line, and you put the imaginary numbers on a vertical axis.
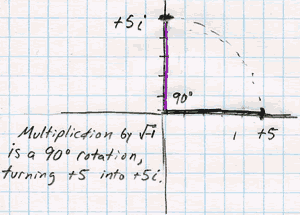
Math
Mystery #2
The
plain truth is, they thought up i because they needed an answer to
the question "What is the square root of -1?" But it begins to make
some sense if you return to the idea that multiplication by -1 is
a 180° rotation about the origin. By this logic, the square root
of -1 (i) would have to be a 90° rotation. Where does that put
you? Sticking straight up out of the origin. This is the imaginary
dimension.
Both
these insights come courtesy of George Lakoff and Rafael Nunez, co-authors
of "Where Mathematics Comes From," a book on math cognition
that seems to be about to become a national bestseller. Their premise
is that all math has bases in the logic of the physical world. One
simple example is the idea that more is "up" and less is "down." For
example, prices "rise" and supplies "drop." Says Lakoff, "In no language
in the world is this convention reversed." The idea is that math concepts
like more and less tie directly to physical realities, for example,
the level of water in a jug. Haven't read it yet, but it could be
a cure for yet more nagging math mysteries.