 Originated
by the French mathematician Rene Thom in the 1960s, catastrophe
theory is a special branch of
dynamical systems theory
. It studies and
classifies phenomena characterized by sudden shifts
in behavior arising from small changes in circumstances.
Originated
by the French mathematician Rene Thom in the 1960s, catastrophe
theory is a special branch of
dynamical systems theory
. It studies and
classifies phenomena characterized by sudden shifts
in behavior arising from small changes in circumstances.
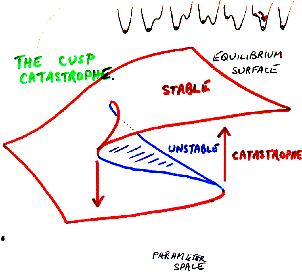
Catastrophes are
bifurcations
between different equilibria, or fixed
point attractors. Due to their restricted nature, catastrophes can be classified
based on how many control parameters are being simulataneously varied.
For example, if there are two controls, then one finds the most common
type, called a "cusp" catastrophe. If, however, there are
move than five controls, there is no classification.
Catastrophe theory has been applied to a number of different phenomena,
such as the
stability
of ships at sea and their capsizing
,
bridge collapse, and, with some less convincing success,
 the fight-or-flight behavior of animals and prison riots.
the fight-or-flight behavior of animals and prison riots.
|