Box o’ Math:
The Hubble Constant and the Age of the Universe

Cosmologists today calculate the age of the universe by using data collected from a broad sample of galaxies. They measure the distance between our galaxy and other galaxies, and the velocity at which other galaxies speed away from our galaxy, and then combine this data to figure out the universe’s age. But how exactly is this data combined?

Let’s start with a basic mathematical relationship: The distance covered by any object moving at a constant rate (like a car or a jogger) divided by its velocity gives you the time it's been moving.

In equation form, this relationship is:

Time = Distance/Velocity

We can also relate this equation to the expansion of galaxies. Since all of the galaxies in the universe exploded into being at the same time (that is, at the Big Bang) and have been moving apart ever since, we can mathematically express the time ( t ) it takes for a galaxy to move away from our galaxy, the Milky Way, as:

t = d / v

where d is a galaxy’s distance from our galaxy, and v is a galaxy’s velocity moving away from our galaxy. (This equation assumes that a galaxy moves at a constant velocity.)

It’s tempting to conclude that this t represents the age of the universe (since our galaxy started at the same point as every other galaxy at the beginning of time). But because different galaxies move at different velocities, we can’t calculate the age of the universe by using this equation alone. Instead, we must first estimate an important number known as the "Hubble constant."

In the 1920s, astronomer Edwin Hubble spent a great deal of time measuring the distances and velocities of galaxies.
When he examined his data, Hubble found that the more remote a galaxy, the faster it was moving away from us--one of the most important discoveries in 20th-century astronomy.

What's more, when Hubble divided the measurement of each galaxy's velocity by its distance, he found that the result was similar for almost all the galaxies he examined. In other words, there appeared to be a relatively constant value--today called the Hubble constant--that related galactic velocities and distances. Expressed in mathematical terms, this relationship is:

v = H x d

where v is a galaxy's velocity relative to our galaxy, d is a galaxy's distance from our galaxy, and H is the Hubble constant.

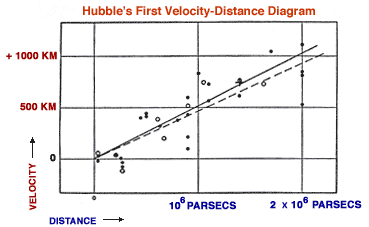
Hubble estimated the constant by plugging his velocity and distance data into this equation, solving for H , and averaging the H values for all the galaxies he measured. Since Hubble's time, scientists have made increasingly accurate estimates of the Hubble constant by combining data from remote galaxies. Powerful, precise instruments such as the Hubble Space Telescope have collected this data.

What does the Hubble constant tell us about the age of the universe?
Quite a bit. But we need to do just a bit more math.

Let's go back to our original time equation, t = d / v . We can substitute for the velocity variable ( v ) in this equation with the " H x d " expression in our Hubble constant equation. The substitution looks like this:

t = d / v becomes t = d /( H x d )

Since we’ve combined the Hubble constant into our time equation, and incorporated our spectrum of galactic data, we can now use our time variable ( t ) to represent the age of the universe.

In fact, it turns out that the age of the universe is simply the reciprocal of the Hubble constant!

t (age of the universe) = d /( H x d ) = 1/ H

So the next time you read about the latest estimates for the age of the universe, you'll know that scientists arrived at them by calculating the Hubble constant and then taking its reciprocal--right?

Well, not precisely.

Combining our two equations to compute the age of the universe only works if we assume that galaxies move at a constant rate. Researchers have recently discovered, however, that a galaxy's speed can vary--which means that scientists have to use even more complicated calculations to adjust their results. Nonetheless, the remarkable Hubble constant has given us a foothold in answering one of the biggest questions of science.

[close this window and return to "Zeroing In"]

©2001 - The Exploratorium