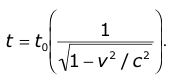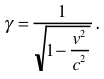Voyage to Epsilon Eridani 3: Time

You can calculate how much time slows aboard a moving ship using your imagination and a little high school geometry and algebra. You’ll end up with the same equation that Einstein did back in 1905!

Start with Einstein’s two basic assumptions:

The speed of light is the same for all observers.

The laws of physics are the same as long as you’re traveling at a constant speed.

We’ll show you one way to derive the formula that lets you calculate how the time measured by the clock aboard your speeding spaceship differs from the time measured by an Earthbound clock.

First, use your imagination.

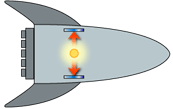
Imagine you have a spaceship like the one you just flew to Epsilon Eridani 3. On this ship, you have a very simple clock. It’s made of two mirrors, set one above the other, exactly parallel to each other. Between these mirrors a pulse of light bounces up and down, making the clock tick every time it hits a mirror. Doesn’t get much simpler than that!

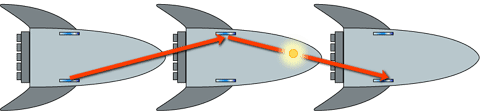
When the spaceship is on Earth, waiting to take off, both a person on the ship and an observer outside the ship will agree that it takes a certain time (let’s call it t ₀ ) for the clock to tick. No surprise there.

The situation changes, though, when the ship flies past an Earthbound observer. From the point of view of the person on the ship, nothing is different: the pulse of light bounces up and down, just as it did before, with the time t ₀ between ticks. But here’s what the Earth-based observer sees:

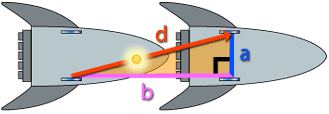
From the Earth-based observer’s point of view, the light pulse travels on a diagonal path between the mirrors as the ship moves forward. This diagonal path is longer than the straight up-and-down path observed by the person on the ship.

Remember that we’re assuming the speed of light is the same for all observers. Both people observe light traveling at about 300 000 kilometers per second. But the Earthbound person observes the light traveling a longer distance for each tick of the clock. Since the speed of light is always the same, it must take a longer time to travel this greater distance. Therefore the moving clock ticks slower for an Earthbound observer than it does for an observer on the ship. Physicists call this effect time dilation.

Now do the math.

Here’s a diagram of the ship moving forward.

We’ve drawn a right triangle made up of three lines:

• Line a, which is the distance the pulse of light moves on its vertical path.

• Line b, which is the distance the ship travels in one clock tick.

• Line d, which is the distance the pulse of light moves on its diagonal path.

If you know the velocity of the ship and the speed of light, you can figure out the length of each line in the triangle. All you need to know is how to convert time and speed to distance. You probably know that if you travel 60 kilometers per hour for 2 hours, you’ve traveled 120 kilometers. You calculate the distance by multiplying velocity by time: 60 kilometers per hour times 2 hours equals 120 kilometers.

Now that you know how to calculate distance, you can figure out the distances in the triangle. Line a, the distance the light travels vertically, is the velocity (the speed of light, or c ) multiplied by the tick time t ₀ that’s observed by a person on the ship:

a = distance the light travels vertically = ct ₀ .

Line b, the distance the ship travels in one tick of the clock ( t, as measured by the Earthbound observer), is velocity v multiplied by the time the clock took to tick t:

b = distance the ship travels = vt.

And line d, the distance the pulse of light moves on its diagonal path, is the velocity (again, the speed of light, or c ) multiplied by the time it took the clock to tick as measured by the Earthbound observer. That’s

d = distance the light travels diagonally = ct.

Now we want to find a relationship between t and t ₀ . The Pythagorean theorem, which you learned in geometry, shows the relationship among the sides of a right triangle.

According to the Pythagorean theorem,

d ² = a ² + b ²

Now you can substitute in the distances you calculated above. You get

( ct ) ² = ( ct ₀ ) ² + ( vt ) ²

With a fair amount of algebraic maneuvering , you can change this equation into

Finally, we have an equation that tells us how long the clock will take to tick t given the time-aboard-ship tick t ₀ and the speed of the ship v. The speed of light c is a constant.

What happens as the velocity of the ship v approaches the speed of light c ? The quantity v ² gets closer to the quantity c ² . Therefore v ² / c ² approaches 1 and (1 – v ² / c ² ) approaches 0. So does its square root. Anything divided by a number that approaches zero gets very large and approaches infinity. And in our equation, the shipboardtime ( t ₀ ) is being divided by a number that’s approaching zero. So, as viewed from Earth, the faster the ship moves, the longer the clock takes to tick ( t ).

Another way to write this equation is

You can separate the right side of this equation into two parts—time and a quantity that physicists call gamma ( ):

Then you can write the time dilation equation as t = t ₀ .

You’ll find gamma in other calculations related to special relativity. You’ll see it in the equations that show how mass increases and length contracts with increasing speed. Once you know the value of gamma, the math for time dilation and other aspects of special relativity becomes very simple.