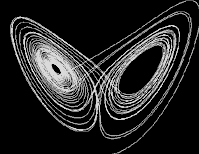
In the early 1960's using a simple system of equations
to model convection in the atmosphere, Edward Lorenz, an MIT meteorologist,
ran headlong into "sensitivity to initial conditions". In the
process he sketched the outlines of one of the first recognized
chaotic attractors
.
In Lorenz's meteorological computer modeling,
he discovered the underlying mechanism of
deterministic
chaos
: simply-formulated systems with only a few
variables can display highly complicated behavior that is unpredictable.
 Using his digital computer, culling through reams of printed numbers
and simple strip chart plots of the variables, he saw that slight differences
in one variable had profound effects on the outcome of the whole system.
This was one of the first clear demonstrations of sensitive dependence on
initial conditions. Equally important Lorenz showed that this occurred in
a simple, but physically relevant model.
Using his digital computer, culling through reams of printed numbers
and simple strip chart plots of the variables, he saw that slight differences
in one variable had profound effects on the outcome of the whole system.
This was one of the first clear demonstrations of sensitive dependence on
initial conditions. Equally important Lorenz showed that this occurred in
a simple, but physically relevant model.
He also appreciated that in real weather situations,
this sensitivity could mean the development of a front or pressure-system
where there never would have been one in previous models. In his famous
1963 paper Lorenz picturesquely explains that a butterfly flapping its wings
in Beijing could affect the weather thousands of miles away some days later.
This sensitivity is now called the "butterfly effect".
Here is a
Java
simulation
of the Butterfly Effect using the
chaotic attractor
that Lorenz
discovered.
|
